自学统计物理和固体物理的时候总是会碰到化学势，虽然其涉及的基本数学推导过程都已经熟悉，但仍然对它的物理意义困惑，它常见的表达式是吉布斯自由能对成分的偏微分，又可以由巨正则分布公式得到它是引入一种成分后系统总能的变化，但却总不能像常见的能量，温度之类物理量一样将其深入理解，也仅仅只能将它当做类能量物理量将其处理，不知道有没有更直观深刻的理解方法？ @傅渥成@何史提@Zeldovich Yakov@Tianqi Chen

从定义上看，“化学势”和粒子数有关，具体来说，是粒子数目的变化导致的Gibbs自由能的变化。但这还是不能更直观的理解它到底是什么。好，在具体的例子中，特别是涉及到粒子数目变化的例子中理解“化学势”，会很直观。

最简单的例子是：单一物质处于气－液两相共存态（vapor-liquid coexistence）

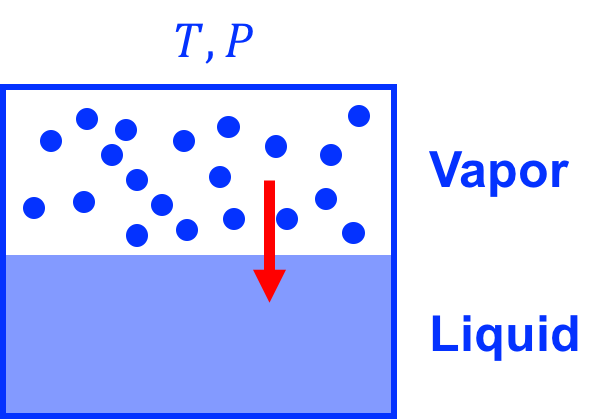
在这种共存态中，个粒子处于气态，个粒子处于液态，并且满足。各自的Gibbs自由能表达式为和。假设某一时刻有个粒子从气态进入了液态，并且，。这必然会导致气－液共存系统的Gibbs自由能发生变化：

利用Taylor展开：

（I）对于稳定的气－液共存态，系统Gibbs自由能对于的扰动应当变化为0，因此：

（II）如果 ，那么，也就是说分子从气态进入液态是允许的。

（III）如果 ，那么，也就是说分子从气态进入液态是不被允许的。

从上面的讨论就可以看出来：

气－液平衡的条件是气态的和液态的相同；

对于未平衡的体系，分子是从具有较高的相流向较低的相。

这个，就是化学势。

其实，系统中存在“化学势”的差异，就是一种驱动分子在不同相之间转移的动力，最终使系统中各处的“化学势”处于相同，即系统达到稳定。

溶液中的溶质存在浓度差异时，粒子会从浓度高的区域流向浓度低的区域。对于理想溶液，组分的化学势确实正比于浓度的对数；对于简单的理想气体模型，化学势正比于密度的对数。这些都表明，“化学势”的差异，驱动了分子在系统内不同相之间的“流动”。

考虑到，大概可以把化学势理解为在维持总能量和能级不变的情况下，衡量体系粒子数和混乱程度之间关系的物理量？

在不变的情况下，不可能和没有关系，那么就把它们之间的依赖关系用来描述？

---------------------------------------------------------

突然想到了温度的定义。那么就试着从热力学的角度给一个理解吧。

这里化学势的定义和温度的定义也是很类似的（温度是什么实际上并不是很显然的问题）。热力学第零定律告诉我们有一种叫做热平衡的状态，达到热平衡的两个物体之间不交换热量，这样的话我们就可以给每个物体贴上一个叫做温度的标签（规定温标）满足热量只从这个标度高的物体向这个标度低的物体转移，而在两个标度相同的物体之间不发生转移。

同样，对于化学势，我们考虑两个可以相互交换粒子的系统。实验上发现，两个系统在某种情况下相互交换粒子的宏观表现为0，达到动态平衡，我们就可以说这两个系统必定有某个量相同，并把这个强度量称为化学势。

推而广之，对于任何一个广延量X，和两个可以“交换”X的系统，都会在某种情况下达到动态平衡，也就对应着两个系统此时拥有的一个相同强度量Y。在X是热量的情形下，Y是温度，X是体积的情形下Y是压强，X是粒子数是Y就是所谓的化学势了。

上面的定性分析实际上并没有给出化学势的具体公式。实际上如果只考虑单一广延变量的情形，作为衡量强度的标度并不是唯一的。比如给定了一个温标T，那么任何关于T的单调递增函数f(T)都可以作为温标（化学势同理）。但我们总是希望找到一些好用的衡量强度的标度，一个比较有效的办法是将同能量联系起来。于是就有了。剩下的就是算算算了。

两个子系统间存在能量交换，那么可以定义一个量温度，温度相等时两边平衡。

如果两个子系统之间除了能量交换还能进行体积交换（比如两部分气体中间连一个活塞），那么就算温度相同也不一定平衡。我们可以再定义一个量叫压强，压强相同时两边就平衡了。

如果两个子系统还可以交换粒子数，那么相应的可以再定义一个东西。这东西就叫化学势。

化学势本身可以理解为一种广义力，对于一个电荷体系，假定整个体系的电势能为： ， 表示位置，则该体系受到的静电作用力为： ( 表示该体系的电势能V对位置x求梯度）， 倾向于做功使体系改变其位置，以降低体系的电势能，体系平衡的条件为： 。

同样的，对于一个共有a种组分的化学体系，不同物质组分的物质的量为 ，体系的自由能为 ，则可定义驱动化学反应的广义力为: ( 表示该体系的自由能G对该化学体系的物质组分求梯度），广义力 倾向于做正功，改变体系的物质组分，以降低体系的自由能，使体系的能量贬值，保证体系的化学反应服从热力学第二定律。很显然的，平衡的条件为： ,即体系的总化学势=0，系统广义上“受力平衡”。

在第一部分，为了对化学势进行解释，引入了自由能的概念。于是，很自然地会产生这样一个问题：自由能是什么？为什么要引入这样一个概念？这一部分便着重回答这个问题。

对于化学反应体系本身，整个化学反应从开始到结束，体系总的熵变为：

，

其中： 为可逆性熵流，表示体系在化学反应中因与外界交换物质与能量而流入体系中的熵；

为不可逆性熵产，表示因化学反应本身的不可逆性而“凭空”产生的熵。

热力学第二定律要求: 必须 ，即任何化学反应都是热力学不可逆过程，必须有新的熵“凭空”产生。

于是，对于等温等压条件下的封闭容器中（若是其他条件则需要另外讨论）的化学反应，根据能量守恒定律：

有 ，其微元关系为： （注意：此处 表示微元， 表示全微分，两者含义不同。因为 不是状态量，严格来讲不存在全微分。以下，凡是不存在全微分的量均用 表示，存在全微分的量则用 表示）

即：体系吸取的热量=系统的焓变。焓就可代表系统的能量。

对于等温等压条件下的封闭容器，唯一与外界环境发生关联的是体系吸取的热量 ,所以体系的可逆性熵流 必然蕴含于 吸收的热量 之内。关于这两者，存在如下关系：

，

这一表达式的含义是：体系在从状态 变化到状态 的过程中，只要吸收外界热量就会使得外界的熵流入体系内。

将体系焓变 的表达式带入 的表达式中有：

；其微元关系为：

移项得： ；

很明显地， 这一项具有能量量纲。它与体系不可逆性熵产 相互关联。前面提到： 表示因化学反应本身的不可逆性而“凭空”产生的熵，是热力学第二定律的体现。而热力学第二定律造成的结果就是能量贬值：原本“自由的”容易利用的能量，转变为了“封闭的”难以利用的能量，降低了体系对外做功的能力。

因此，在准静态过程的假设下，可以定义新的状态函数——自由能： ， 表示体系中未贬值的能量；

因此： 表示：体系因为发生了热力学不可逆过程（化学反应）而被热力学第二定律强行贬值的能量，化学反应的后果就是使得体系的可用能量（自由能）减少，体系做功的能力降低。

有了以上的分析，让我们再次回到化学势的概念上来，第一部分提到：化学势是一种广义力 。则 做的功可以表示为： ,即：广义力 做功会使得体系的自由能降低，使得体系的能量发生贬值，“自由”可用的能量减少，体系“凭空”产生了新的熵。这是热力学第二定律在化学反应中的体现。即：化学反应是广义力 做正功的结果，也总是向着广义力 正功的方向进行。当广义力 时，反应达到平衡态，广义力不能再继续做功了，体系对外做功的能力为0。

另外，需要注意的是，以上的推导均是在“等温等压条件下的封闭容器中的化学反应”这一前提下进行的，若化学反应发生于其他条件之下，则 、 、 、 等物理量的表达式将发生变化。相应的广义力 也需要重新定义。

在第二部分， 被直接 称为自由能，而非吉布斯函数或者吉布斯自由能。这是因为：自由能与吉布斯函数并非始终等同。为了描述清楚两者的关系，重新约定：

为体系的自由能；

体系的吉布斯函数；

在热力学中：

体系的焓定义为： ;

体系的吉布斯函数定义为： ;

对 与 进行全微分有：

在既不等温，也不等压的封闭容器中的化学反应，依旧有能量守恒关系：

（若容器为开放容器，则 。此时还需要考虑与外界的物质交换所造成的熵流。熵流本身可正可负，为正则表示环境中的熵流入体系内部，为负表示体系中的熵流出到环境中）；

于是： ，将之带入吉布斯函数的全微分式中，有：

第二部分提到： ，最终可以得到，对于既不等温，也不等压的封闭容器中的化学反应，有：

因此在既不等温，也不等压的条件下，封闭容器中的化学反应体系的 ，而是相差了 这两项，吉布斯函数中广义力 所做的功被体系温度和压强的变化所“遮盖”。此时， 不再是热力学第二定律的体现，也就不能用于化学反应方向的判定。

只有在等温等压封闭容器的条件下( 且 )，才有 。

在这个部分，依旧约定：

为体系的自由能；

体系的吉布斯函数；

对于一个实际的化学反应： ，在发生化学反应时，在 时间内，A、B、C、D四个组分物质的量的变化，可以写成一个向量：

为了讨论方便，引入化学计量数向量： ,约定反应物的化学计量数为负，生成物的化学计量数为正。并引入反应进度 的概念，定义：

于是：

；

第二、三部分提到，热力学第二定律始终要求： ，因此自然有 ，于是就得到了热力学第二定律在化学反应中的描述： 。

于是在计入化学计量数约束的条件下：

表示化学反应自发正向进行；

则表示化学反应达到了平衡态（不同于无约束条件下的 的条件）；

表示化学反应正向进行时会违反热力学第二定律，于是化学反应只能自发反向进行。

同样的，在等温等压的封闭容器中，有 。

化学势在热力学里非常容易理解，就是Gibbs自由能对原子数（视为实数）的偏导数。根据推导，还可以推出其另外三个等价定义。关于化学势的应用，朗道给了许多有意思的例子。

统计物理中要注意，用巨正则系综是无法推导出来化学势的，化学势在巨正则系综中是个自变量，可以随意取值。只有在正则系综中可以得到。但是对于粒子数可变的系统，从正则系综出发，又难以推导相关配分函数。只好用巨正则系综推导配分函数、再用拉普拉斯逆变换到正则系综、再计算化学势的曲折办法。Am. J. Phys.有一篇B. McCoy写的文章，详细介绍了这套计算，并用Mathematica算出了费米子、玻色子理想气体的化学势随温度变化。

做分子动力学、萌卡、相场计算的话，化学势也很容易理解，可以用模拟计算得到的数据获得化学势信息。phase field计算专家陈龙庆老师有一篇文章，从热力学角度讲解化学势，简单直观。

但到了“量子多体理论”中，它的出现就非常神秘了。我旁听同事讲的QMB课程，似乎是由Lagrange乘子法引入了一个参数，这个参数就叫做化学势。在BEC相关的计算中，就这么跳出来了。更加“物理”的讲解我还没见过。也是我QMB、半导体物理相关文献读的少，无法多谈。希望各位专家能深入谈一下。 @浅斟低唱 @Narayan @kBlnW

上一篇：MYT时间与麦加时间换算

下一篇：一图读懂！香港特区选举制度改革解读